Quantum Quickies #1
Quantum Quickies #1
The qubit: the unit of information for quantum computation
Well, the results of the survey for input on future directions of The Quantum Stack are in. As you can see below, it sounds like there’s a lot of interest in the Waves of the Future concept, followed by both Quantum Quickies and The Quantum Journeyman.
Given this, I do plan to launch a Waves for the Future series. (First topic: meet LOWESA, a newly-introduced classical algorithm for approximately simulating quantum computers.) In the meantime, I think also exploring the Quantum Quickies concept is interesting and potentially useful. (Recall that series is for shorter articles introducing core concepts from quantum mechanics and quantum computing1.) Given the length constraint, covering a topic in full detail isn’t feasible. So instead, I plan to share some interesting/salient thoughts, and offer references for further reading.
Today’s Quantum Quickies topic is the qubit (pronounced “cue-bit”, not “quib-bit” or some other such thing). Qubits are the units of information for quantum computers, quantum networks, and quantum communication protocols. They are often described as the quantum analogue of the classical bit.
What makes qubits powerful?
There are things you can do to qubits – such as put them in superposition states, interfere their states, or entangle their states – which you cannot do classically. These properties are part of what makes qubits (or rather, the quantum computers built out of them) powerful. I plan to cover each of these ideas in a subsequent Quantum Quickie article.
It’s commonly stated that one reason qubits are powerful is that if you have n qubits, you need an exponentially large number of variables to describe an arbitrary state of them. While this is, strictly speaking, true, it’s also true of so-called probabilistic bits. So in that sense, the exponential growth in the complexity required to describe arbitrary states of n qubits doesn’t necessarily yield (on its own) a more powerful compute resource.
Taken together though, the exponential growth of quantum state space as you add qubits, along with the ability to do superposition, entanglement, and interference, does give a computational resource which has provable advantages over purely-classical (digital) computing. I plan to cover the topics of quantum circuits, algorithms, and speedups in subsequent Quantum Quickies articles.
How do you build qubits?
Any quantum-mechanical system possessing at least two distinct states could be used as a qubit. As such, there are many qubit modalities (types) being investigated and developed by the academic and commercial quantum technology communities. You may have heard of some of them before:
Superconducting circuits
Trapped ions
Neutral atoms
Quantum dots
Nitrogen vacancy centers
Photons
A helpful image developed by Michel Kurek of LeLabQuantique a few years ago highlights both the modalities and various organizations which are building quantum computers using them.
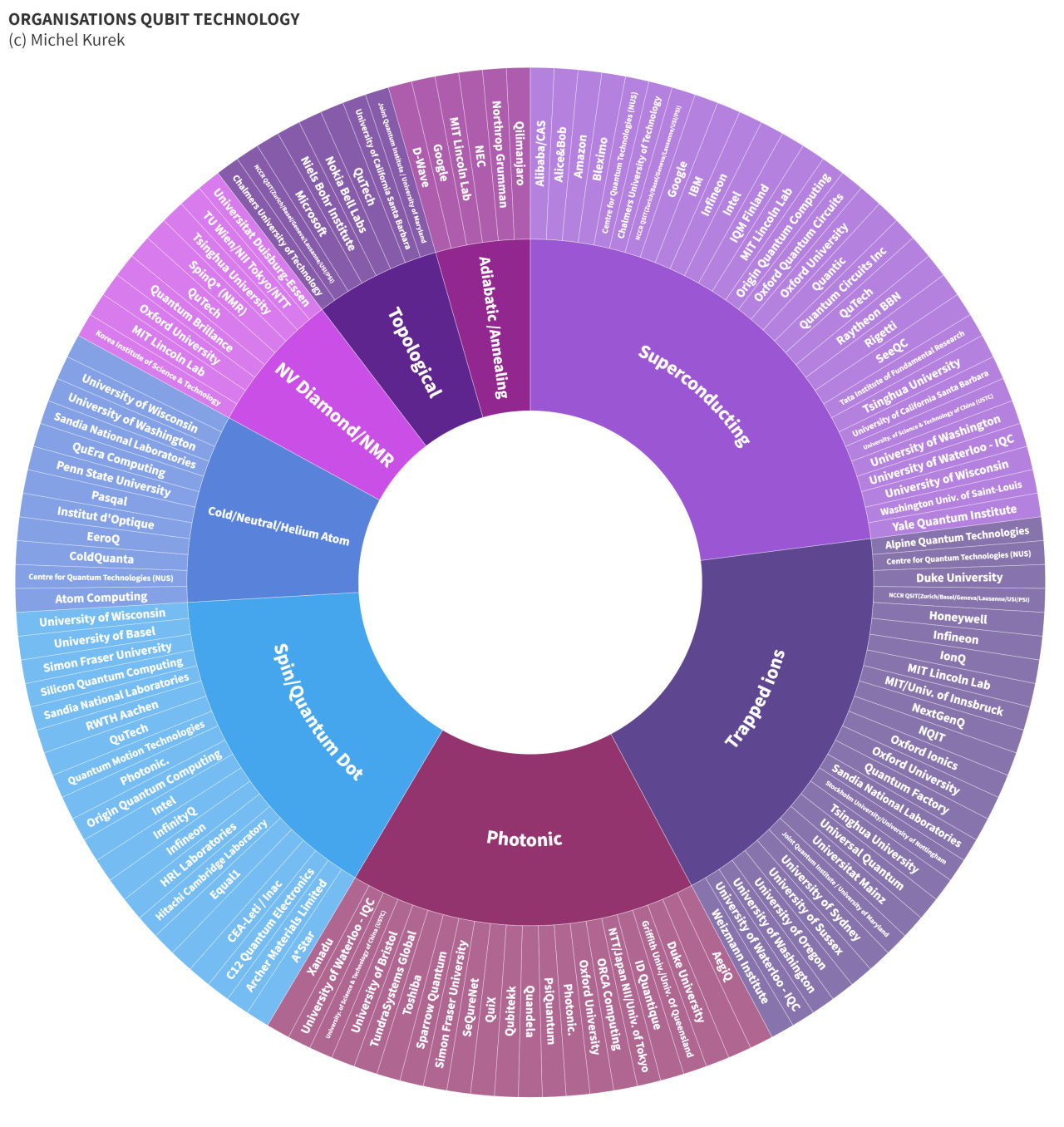
As you can see, there is robust activity in all qubit modalities. You might be wondering which modality is “the best”. The answer at this time is ‘It depends on what you care about’. Each modality has its own strengths and weaknesses. Some can operate at higher clock speeds than others. Some are more stable than others. Some require large-scale cryogenic equipment; others do not. Some still need their fundamental physics to be further studied; others are more mature. Some occur ‘naturally’ in nature; others are engineered. Some can leverage standard semiconductor manufacturing processes; others require new approaches.
You might be wondering which modality is “the best”.
The answer at this time is “It depends on what you care about.”.
In addition, it’s already recognized that realizing large-scale quantum computation is going to require converting information encoded in one qubit modality into information encoded in another. This process (called transduction) is needed to, for example, network quantum computers together or store information transmitted over a quantum communications network. So in that sense, the future of quantum computing is at least 2 modalities working together.
If you wanted to learn more about various qubit modalities, here are some review articles:
A Quantum Engineer’s Guide to Superconducting Qubits & Superconducting Qubits: Current State of Play
Quantum Computing with Trapped Ions & Trapped-Ion Quantum Computing: Progress and Challenges
Quantum Computing with Neutral Atoms & Quantum computing with atomic qubits and Rydberg interactions: progress and challenges
Photonic quantum information processing: a review & Photonic Quantum Technologies & Photonic Quantum Information Processing: A Concise Review
Semiconductor Spin Qubits & Semiconductor Qubits In Practice
What makes a ‘good’ qubit modality (or proposal)?
Notwithstanding the above, there are some desiderata which have been identified as to what all qubits need to have in order for them to be ‘good’ ones for realizing quantum computation. These desiderata are a subset of the DiVincenzo criteria, a set of criteria identified by physicist David DiVincenzo over 20 years ago in the paper The Physical Implementation of Quantum Computation.
There are 5 (plus 2) criteria DiVincenzo identified. I’ve lifted the criteria directly from the paper; the commentary is my own.
A scalable physical system with well characterized qubits.
The modality needs to be scalable – you have to be able to put more qubits in the computer. And those qubits need to be ‘well-characterized’, meaning you understand the physics of the modality well enough to understand how those qubits will behave, and that you can ensure the computation taking place on those qubits doesn’t cause the information to ‘leak out’ to other quantum states the modality could support (but which aren’t used for computation).
The ability to initialize the state of the qubits to a simple fiducial state.
For most modalities, the qubit is encoded in the lowest and second-lowest energy state of the system. Commonly, the ‘simple fiducial state’ used is the lowest-energy state. Initialization procedures include simply letting the qubits relax to that low-energy state, or measuring them and actively resetting them.
Long relevant decoherence times, much longer than the gate operation time.
Decoherence is a kind of noise affecting qubits. Long decoherence times ensure you can complete a computation (circuit or algorithm) before all the ‘quantumness’ of your qubits has been destroyed.
A “universal” set of quantum gates.
In order to realize arbitrary quantum computation, you need to be able to perform arbitrary operations on qubits. It turns out, though, that as long as you can implement a specific (and finite) set of primitive operations, you can compile arbitrary operations onto that set and thereby realize universal computation.
A qubit-specific measurement capability.
You need to be able to read out the state of the qubits. How you do so depends on the modality.
The ability to interconvert stationary and flying qubits.
This is the transduction problem noted earlier. As the names imply, ‘stationary qubits’ would mean those qubits in the quantum computer, and ‘flying qubits’ would mean those qubits which are transmitted across a network from one computer to another.
The ability faithfully to transmit flying qubits between specified locations.
Phrased another way, whatever mechanism is being used for quantum networking needs to work well (have high efficiency, support a sufficient data transfer rate, etc.).
Wrap up
In this inaugural Quantum Quickies article, we covered the topic of the qubit, the foundational building block of quantum computers. Qubits possess many interesting properties, such as being able to be put into superposition, or being entangled with one another. These properties (and others) enable qubits to store process information in ways which are advantageous compared to classical bits. There are many proposals out there for the physical substrate/foundation (aka modality) upon which to build qubits. Each has their own pros and cons, though it’s clear that the future of quantum computers – depending as it does on networking quantum computers together – could require at least 2 modalities to work in concert with one another. The DiVincenzo criteria spell out what’s necessary to realize quantum computation in a physical (as opposed to abstract) setting, and provide a set of desiderata that a modality (or specific implementation proposal within a given modality) needs to satisfy to be ‘good’ for quantum computing.
What did you think of this article specifically, and the idea of Quantum Quickies more generally? Let me know in the comments!
A shout-out to a certain special someone for co-creating with me the logo for this series. You know who you are…