Quantum Machine Learning - An Introduction
Quantum + ML = ??
Welcome! This is The Quantum Stack. Created by a Travis L. Scholten, it brings clarity to the topic of quantum computing, with an aim to separate hype from reality and help readers stay on top of trends and opportunities. To subscribe, click the button below.
Tell me, truly – when you read the title of this post, what did you think? Were you interested? Suspicious? Maybe a little incredulous? For what it’s worth, someone else has probably though similar, so you’re not alone.
You might be concerned that the topic of quantum machine learning (QML) is full of hype, not really applicable to any practical problems, or some odd combination of both. The purpose of this piece is to give you enough of an overview of the topic so you have a grounding in it, and can better understand how QML breaks out into distinctive, comprehensible categories.
Note: This post is going to be a bit more link-heavy than usual, because providing references and further reading is important for this kind of post, in my opinion.
QML: The big picture
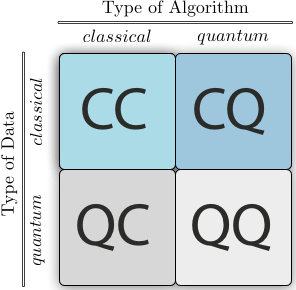
The easiest way to understand QML is to understand the chart above. I’ve cribbed it from the Wikipedia article on the subject. As you can see, it breaks up QML into two categories, and within each, asks whether something is classical or quantum in nature.
One category is the kind of data being processed (vertical axis). Here, “classical” data is pretty self-explanatory: it’s the world we’re familiar with: images, text, audio, etc. Anything that is, at its core, stored as classical bits would fall into this category. However, “quantum” data is a bit more opaque. It turns out “quantum” data needs to mean 2 things: quantum states themselves (for example, prepared by a quantum computer, or coming from a quantum sensor or communications link), or classical data obtained by measuring a quantum state.
The second category is the kind of algorithm used to process the data (horizontal axis). Here, a “classical” algorithm means any algorithm which uses purely-classical computers to run. And a “quantum” algorithm means an algorithm designed to be run on a quantum computer. Quantum algorithms, at their core, use quantum circuits to describe the computation.
For each combination of choices from each category, we get a different sub-category of QML. These subcategories are briefly described below, and we’ll do a deeper dive below.
CC: “quantum-inspired methods”. In this sub-category, we are talking about purely-classical algorithms which process purely-classical data. “So, what does that have to do with quantum?” you might ask. Good question! It turns out there are some ideas from quantum computing and quantum information science that we’ve figured out how to strip out all of the quantum mechanics. What we’re left with is a classical idea or algorithm which has its origins in quantum. Hence the moniker “quantum-inspired”.
CQ: “quantum-enhanced machine learning”. The core idea within this sub-category is to take classical data and embed it into quantum computers through the use of quantum circuits. Then we process that classical data in some way on a quantum computer..
QC: “Machine learning for physics”. This sub-category is about applying classical ML algorithms to process data from quantum computers. Here, the idea is to take whatever data comes from measuring a quantum computer and run it through a classical ML algorithm to make inferences about the behavior of the quantum computer.
QQ: “Quantum Learning”. This sub-category is the most interesting from the perspective of fundamental research in QML, as it focuses on quantum algorithms which process data encoded as quantum states. Here, we typically assume the state is handed to us “for free”, unlike the CQ case, in which the focus is on how to encode and process classical data. For example, the quantum state might arise from some quantum sensor, which is then piped over to a quantum computer via a quantum network.
Having briefly described each of these sub-categories, let’s take a closer look at each.
Quantum-inspired methods (CC)
Quantum-inspired methods draw their inspiration from quantum computing and algorithms. But what does that mean? A couple of examples will clarify things.
The first is the “de-quantization” of quantum algorithms. This line of research burst into the scene with a result back in 2018 from Ewin Tang showing how a quantum algorithm for recommendation systems (aka, solving the Netflix problem) could be turned into a classical one. Incredibly, this result showed the resulting classical algorithm was faster than any known to that point, and also only slightly slower than the quantum algorithm it was inspired by. Tang’s result has inaugurated a line of work in which researchers try to de-quantize other quantum algorithms.
This kind of work – while depressing in the sense of “Those darn classical algorithms are getting better compared to quantum!” – is quite useful, precisely because it helps us understand the performance gap between classical and quantum computers. Further, as quantum algorithms are de-quantized, the ones which remain (and their associated provable speedups) give us a better sense of what kinds of computational tasks are actually amenable to quantum.
The second example is the introduction of tensor network methods in classical AI. Tensor networks are a kind of classical data structure physicists created to study the behavior of highly-correlated quantum-mechanical systems (e.g., spin chains). These data structures have tunable properties which allow them to capture different kinds of correlations in the system. Interestingly, the use of tensor networks has emerged as an alternative to some existing approaches in classical ML. If you want to know more about tensor networks, see this site.
Quantum-enhanced machine learning (CQ)
This sub-category has exploded in popularity in recent years, as quantum computing started to make contact with classical data science. The key idea for methods in this category is to simply augment (or “enhance”) classical ML algorithms with access to quantum computers. Some examples of methods in this category include:
Quantum kernels. Kernels are similarity measures between two pieces of data, say x and y; kernels are used quite a lot in classical ML to help boost the performance of the algorithm. Quantum kernels are computed using a parameterized quantum circuit. The resulting similarity measure K(x,y) can be used in any classical kernel-based algorithm. A great overview of quantum kernels can be found here.
Quantum neural networks (QNNs). The literature hasn’t yet converged on what exactly a QNN means, but quantum analogues have been proposed for the classical neuron, convolutional neural networks, and recurrent neural networks.
Quantum generative adversarial networks (qGANs). I call these out as separate from QNNs, because generative modeling has emerged as one of the most interesting ways quantum could be applied to ML. Why? The intuition is quantum computers can generate probability distributions for which classical computers struggle to generate samples. (Though “quantum ChatGPT” is unlikely to be a thing for a while!) Depending on the paper or implementation, a qGAN may use a classical or quantum neural network for both the generator and the discriminator. Examples of qGANs can be found here and here.
One reason why I am particularly excited about this category is the fact that it seems the most straightforward way to connect quantum computing to classical ML without having to wait for fault-tolerant quantum computers. (Such computers are generally required for the algorithms in the QQ sub-category.) Further, there are formal proofs for quantum kernels that they can yield an advantage , though with respect to a highly-contrived classification problem, as well as proofs for quantum generative modeling (though again, with respect to a highly-contrived problem). These sorts of results give us a small toehold on the power of quantum-enhanced machine learning, and also give us new techniques with which we can refine our understanding.
This said, there are definitely some obstacles to using quantum-enhanced machine learning in practice. One of the most prominent ones is the notion of “barren plateaus”, which is the phenomenon that, as the number of qubits in the circuit increases, any gradients with respect to the parameters of that circuit tends to decay exponentially. This makes it hard to train quantum neural networks, because gradient-based algorithms would tend to get stuck. That said, some workarounds have been proposed. Barren plateaus also have implications for quantum kernels; namely, the resulting similarity measure can become easily-approximable by a purely-classical kernel.
Another obstacle is simply a data throughput problem – quantum computers can’t magically process an entire data set at once (it has to be loaded piece by piece, somehow!), meaning the rate at which data can be loaded and processed can form a significant bottleneck in the overall wall-clock time of the algorithm. That is, for these algorithms usually you load a data point (or two, in the case of quantum kernels), and you do some quantum computation, and then you load the next data point(s). This all happens in serial, so the rate at which you can load and process data will become a factor to using these algorithms in practice.
ML for Physics (QC)
This sub-category really isn’t very applicable for end-users of quantum computers, as it is concerned with the use of classical machine learning methods applied to classical data generated by quantum computers. (That is, the output bitstrings which come from measuring a quantum state.) Examples of activities in this sub-category include using machine learning to design quantum computing experiments, characterizing the noise affecting quantum computers, and predicting the capabilities of quantum computers.
Quantum Learning (QQ)
This subcategory can be subdivided in at least 2 ways. The first is some specialized quantum algorithms for machine learning problems, such as linear systems solvers, clustering, and topological data analysis. The second is processing data in the form of quantum states.
The first division is the one you’ll probably commonly hear about when people talk about QML, and one which receives a lot of attention due to the promise (with quite a few caveats!) of exponential speedups for some tasks. In particular, back in 2008, Harrow, Hassidim, and Lloyd proposed an algorithm for linear systems solvers with such an exponential speedup. (For an overview of the “HHL algorithm”, see here.) However, this algorithm relies on a particular data structure, qRAM, for which it is currently unclear if it can be actually implemented at scale.
The two other common ML tasks falling into this division are clustering and topological data analysis. The former is the problem of determining, given a collection of points, the most optimal way to group them, whereas the latter is a family of problems related to analyzing data sets using ideas from topology. A nice discussion of quantum algorithms for TDA is available here.
The second division (processing data in the form of quantum states) seems a bit similar to quantum-enhanced ML (CQ) above. At first glance, both involve encoding data into quantum states, and then doing some processing, so what’s the difference? The primary difference is that in quantum-enhanced ML, we’re encoding a purely classical data set into quantum states, whereas here, the quantum state being processed originates from some kind of quantum-mechanical process.
An example might help – suppose I have a quantum sensor somewhere, whose state changes in response to the environment (e.g., a spin in a magnetic field). I can take that state and send it to a quantum computer (e.g., via a quantum communication link). Then I might run some kind of data processing on that state. Or, as another example, I might use a quantum computer to simulate the time dynamics of a condensed matter or chemical system, then use a circuit to calculate some property of that state. In both of these examples, the state being processed by the algorithm has its origins in some kind of quantum-mechanical system.
Sum-Up: Quantum Machine Learning
Hopefully this post has given you a better handle on quantum machine learning. It is definitely an active field of research, and there are lots of threads researchers are pursuing. (In reviewing the Wikipedia QML article before publishing this post, I see there have been a lot of updates!)
The essential part to remember is there are 4 sub-categories in QML: “quantum-inspired”, “quantum-enhanced”, “ML for Physics”, and “Quantum Learning”. Of these, “ML for Physics” is not useful for end-users, and “Quantum-Inspired”, while having ‘quantum’ in the name, doesn’t use any quantum computers at all. And while there is the most promise for algorithmic speedups in the “Quantum Learning” category, the methods in the “quantum-enhanced” category, while slower, can be much more easily picked up by data scientists and other machine learning practitioners.
QML is also a relatively new-ish field in quantum computing, meaning the full arc of various trends is still being hashed out. For example, do barren plateaus spell the end of trainability of quantum models? Can quantum kernels be meaningfully applied to a practical data set? Are there data sets out in the world which can be well-modeled (in a statistical sense) by the output of quantum circuits? All of these questions are under active research, in a plethora of ways. For a great overview of some of the outstanding challenges and opportunities in QML, see this paper.
To close, I wanted to share this video from Dr. Maria Schuld of Xanadu, a Canadian quantum computing startup. In particular, Maria’s discussion about how the research community can get a handle on some of the core, foundational topics in QML is quite interesting.
P.S. In addition to The Quantum Stack, you can find me online here.
Was this article useful? Please share it.
Note: All opinions expressed in this post are my own, are not representative or indicative of those of my employer, and in no way are intended to indicate prospective business approaches, strategies, and/or opportunities.
Copyright 2023 Travis L. Scholten



Great piece. Sadly, data sets relevant to quantum computing are still relatively un available. Maybe when we start running sophisticated physics experiments in quantum computers - 10 years from now- shall we truly see their relevance.